I have noticed that many entrepreneurs, leaders, and managers have trouble trading off and determining the ideal level of sharing on a particular project. The question becomes how much control should they give up in order to include others in their endeavor.
In the case of an entrepreneur, it’s necessary to understand the relinquishing equity in order to gain the capital or expertise to sustain growth. My experience is that many entrepreneurs start out thinking that they want to maintain 100% of the equity for as long as possible. They struggle with selling or otherwise parting with equity because it would dilute their ownership stake. Their fear is they will lose control and/or a large part of the value if the enterprise is ultimately successful.
Managers are conventionally concerned with complicating decision authority on projects if others are included. If the project is successful, then the credit will be diluted and spread across others.
Basically, as individuals who like to optimize decisions, we should be willing to include others and dilute our equity, control, or authority if we believe that the resulting endeavor will be bigger, more profitable, or more successful.
 I subscribe to a fairly simple model that helps people trade off psychological concerns and make the decision appear more objective or analytical.
I subscribe to a fairly simple model that helps people trade off psychological concerns and make the decision appear more objective or analytical.
I start with the natural premise that there is a pie – money, credit, etc. – that we will be spitting up. At the end of the activity, everyone wants the most pie they can get. It’s a pretty common tactic to seek the largest piece of pie in any deal. So, our goal is to develop a working symbolic model that helps us make decisions about splitting up a pie.
From basic geometry, we know that the area of a pie can be represented as:
Areapie = ᴨ ∙ Radius2pie
Areapie is the total area of pie available as a reward for this project. We would say the “area of a pie is pi times the radius squared.”
If we are going to split the pie into slices to share with others, we still want to maximize the pie we eat. In fact, our goal is that if we offer pieces of pie to others that we get more pie than we had originally. Our plan of action is that we won’t give up pieces of the pie unless we are relatively confident that the slice of pie we are left with will actually be larger than the original total pie since we expect the pie to grow.
Turns out, also from high school geometry, the area of a piece of pie (sector) is equal to:
Areaslice = ᴨ ∙ Radius2pie ∙ Angleslice
We would say the “area of a piece of pie is pi times the radius squared times the angle.”
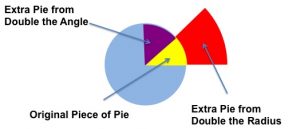
So if we are going to give out pieces of pie to others, we need to know that the area of our new slice is bigger than our old slice, even if the angle is smaller. This is because we expect the pie radius to grow. In fact, we hope the pie will grow very rapidly.
The good news is that a pie grows by radius-squared much faster than by the angle. In fact, things growing at radius-squared are much better than things growing by the angle.
 |
 |
One way of verbalizing the model is:
To entice others to help us grow our endeavor, we are willing to relinquish a proportion of ownership (angle or linear reduction in pie) as long as we are convinced that the resulting growth (radius-squared growth in pie) will more than offset the reduction in proportion.
It’s much better to make the pie radius bigger rather than protect the angle of pie ownership.
Two anecdotes that illustrate my point:
Anecdote 1 — NASA program manager model
Anecdote 2 — Legal Services for Start-Ups
A great example is when the founders/owners of early-stage businesses need to decide if they should dilute their equity and raise more capital. Typically, there is ‘sticker shock’ when the first term sheets arrive. The implied valuation of the company is less than anticipated, meaning that to raise a fixed amount of capital the ownership team will need to give up more of the company – a larger slice of the pie. This can be hard to swallow, and new entrepreneurs are reluctant to give up any stake, especially if control is likely to be threatened in this or future rounds.
Hopefully, the Pie Model presented above will help founders/owners/managers decide whether to take the round of funding or not. One should approach it analytically and not just dismiss the funds due to a principle of not sharing control or simply accept it because one is hungry for a capital infusion.
Sincerely attempt to understand: Will the funds help you grow the pie more than you could without the funding and will the net result be more pie? As they say, 100% of nothing is much smaller than 25% of something. Very few businesses grow without raising funds, so some compromise is needed.
In fact, most venture capitalists (VCs) I know usually try to understand the enterprise risk from four vantage points prior to investing: technical, market, execution, and fundraising. The fundraising risk for future rounds is actually an important consideration. One reason a company may be unable to raise funds is that steady progress is unlikely toward critical milestones that would be appreciated by future investors. These milestones might be technical or customer-oriented.
Another reason a company might not be able to raise funds is that the principals appear to be unwilling to raise additional funds because they are overly concerned with dilution. There are many reasons new funds might need to be raised, such as to fund new opportunities, span the gap of unexpected delays, and changes in markets that require time to change strategies.
If the new venture is unable or unwilling to raise new capital, then the company gets a big black mark. Access to funds is needed, and in most cases, non-dilutive loans from banks will not be able to provide the growth capital. It’s important for founders of new ventures to have a balanced view toward raising dilutive capital as a means of funding growth or spanning the time needed to reach breakeven and beyond.
So, investors like to believe the management team understands that accepting dilution to sustain the growth can be a proper course of action. If the management team is predisposed toward avoiding dilution at all costs, this can be a danger signal and may prevent sophisticated investors from participating.
Advanced Pie Model – Engineers would say that we are trying to make sure that radius-squared growth has to be more than the angle we give up. Or for those who desire an even more rigorous math model, with a little algebra, we can write the following ratio equation: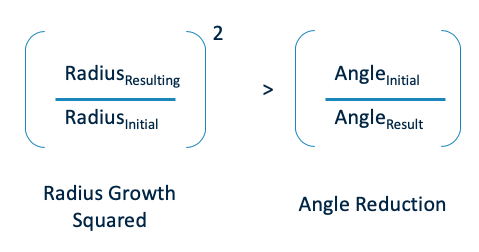
Share this Post

