Discussions about acting and thinking globally vs locally receive lots of discussion in management literature. In fact, this market is well-served by the strategy consulting industry. However, I have heard on many occasions employees spout these concepts while acting contrary to the principles. So, my goal was to develop a couple of models and catchphrases to help employees and managers understand some of the principles and be able to assess their actions.
My favorite model is an analogy to an engineering problem solved by one of my professors. Dr. Arthur “Art” Bryson started his career as an Asst. Professor at Harvard in Applied Math, where he studied applications of linear and non-linear optimization to engineering problems. Young faculty members need to get grants, so he proposed to the Air Force to study aircraft climb optimization. Since they were out to set new “time-to-climb” records with their next generation jet fighter aircraft, they agreed to send a little study money to the new professor.
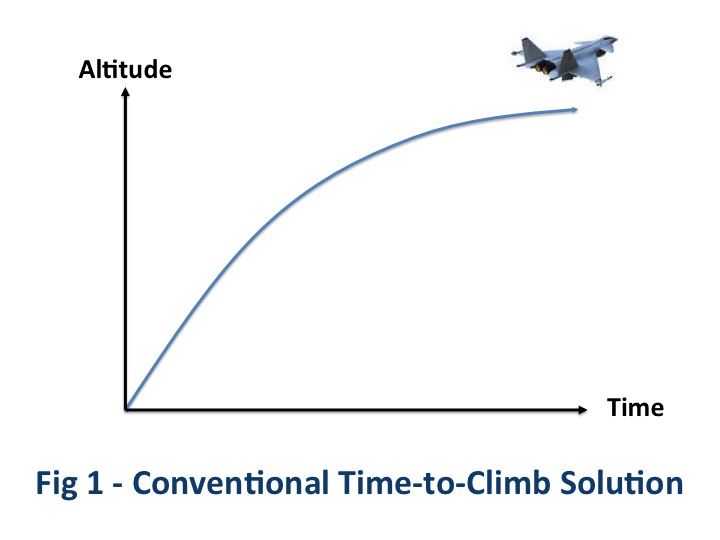
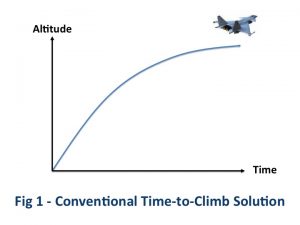The conventional way one would optimize the time-to-climb is to take the aircraft to various altitudes and test the climb rate at various speeds and weights. The goal was to find at every altitude and every weight the ideal speed to fly that would give the maximum rate of climb with full throttle. Ultimately, one would end up with a graph of speeds the pilot should fly at each altitude while climbing at the maximum throttle to the designated altitude in an attempt to set new records for their class of aircraft. The climb profile might be viewed as being similar to the concept illustrated in Fig 1.
Until then, the way a climb profile was made more accurate was by collecting the same data at more altitudes. This process is actually quite complex because the test pilots would have to get the instantaneous best climb rates for a variety of conditions, and the test pilot couldn’t just fly level at the designated altitude and suddenly add power and pull back. The Air Force hoped that the young professor would find a way to smooth the data and reduce the complexity, time, and cost of collecting the data for attempting records.
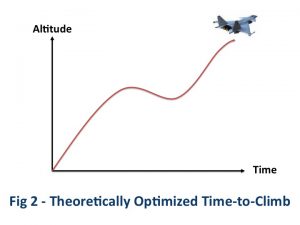Professor Bryson instead used optimization methods coupled with physical models corrected with flight data to compute what he viewed were optimal trajectories. His proposed trajectories were something similar to the climb profile illustrated in Fig 2. He recommended that pilots should level out and even dive for a bit in the middle of the climb as a way to increase performance. This was an astounding prediction.
Conventionally, pilots fly a trajectory so that at every altitude the plane climbs at its maximum climb rate. The quite logical argument was that one couldn’t get better than flying at maximum rate-of-climb at every instant. Certainly, the sum of flying the absolute best at every instant had to give the optimal overall climb rate.
Professor Bryson argued that his optimization algorithm predicted otherwise, and he wouldn’t back down. He believed the math. So, the Air Force scheduled a test and had two pilots fly aircraft competing against each other. I jokingly assert that they probably flipped a coin, and the loser had to fly the junior professor’s algorithm.
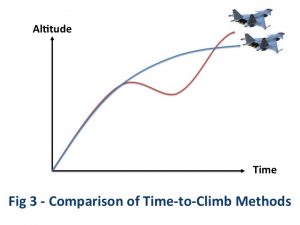
Both pilots took off at the same time and flew identical trajectories in the beginning, but just past the midpoint as the climb rate was starting to decrease, the one flying the professor’s algorithm pushed over the nose and started to dive. The other pilot, I am sure, smirked. But to most everyone’s surprise, after the airplane in the dive picked up speed, she pulled back and passed the other plane quite easily. See Fig 3.
How could this be? How could it be better to do something suboptimally part way through the exercise and end up with a better – optimal – result than someone doing the best at each instant?
Turns out, there is a logical, physical explanation. As a jet aircraft goes higher and higher, the Mach number, i.e., the speed of aircraft relative to the speed of sound, increases. As the jet approaches Mach 1, which is the speed of sound, the drag on the aircraft increases radically. If it goes faster than the speed of sound, the drag falls off and actually reduces. So as an aircraft approaches the speed of sound, it would be best to accelerate as quickly as possible through the ‘sound barrier,’ the drag rise just near the speed of sound.
The airplane on a conventional climb profile did not have sufficient power to accelerate through the drag rise. So, what seemed like a suboptimal procedure, to give up some of its precious altitude and use it to dive through the drag rise, actually improved the overall performance. For a time, the airplane on the new trajectory experienced a setback in performance in order to get a better long-term result.
Afterward, it was easy to explain, and after witnessing it, the logic became clear. Now, it is the standard approach for such record flights in high-performance jet aircraft.
I believe this is a key characteristic for leaders. An essential trait of ‘management’ is helping team members optimize their performance, initially by making sure they are continuously performing at peak performance. But sometimes, it is important to give up some performance for a time to get to a new higher-performing operating condition. Referring back to the airplane climb rate example, if one breaks off into the dive too early, or dives for too long, or waits too late, the conventional climb profile will clearly win.
So, leaders must constantly assess when the best time is to invest in the tools, process, or people to get better overall results. In real life, no exact formula exists, but skilled leaders develop a set of assessment tools, combined with intuition, to determine the best time to break with convention.
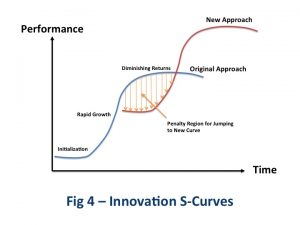It is quite common in management books to talk about Technology or Product S-Curves. These are the curves that a particular technology or product will follow during its maturity cycles, which are simplistically illustrated in Fig 4. This concept can easily be extended to management approaches. The key decision is to know when to pay the penalty for jumping to the new S-curve. I find the airplane climb example makes it easy for me to think of the decision process and try to find the right timing for the particular situation at hand.
One example of an internal decision that requires timing is switching to a new management data processing system such as an Enterprise Resource Planning (ERP) system. It is typically time-consuming and costly to develop the processes, procure and implement the software, convert the data, debug the system, and then train the users. However, once all those steps are completed, the hope is that the benefit to the organization will be huge, and the payback will accrue quickly.
An example of one that is harder to assess is when to launch a new product. It is clear that launching the product is likely to cannibalize sales, and it may even result in some performance reductions. So, the natural tendency is to want to delay such a product introduction. On the other hand, in a competitive market, one’s competitors might jump onto the new technology curve and make the current product obsolete, leaving the laggard behind. Trying to choose the correct time given external movers is challenging. One interesting example is when Apple decided to replace its very successful OS 9 operating system with OS X, a Unix-based system. At the time, most decried the decision and predicted the demise of the Macintosh. History, however, shows that Apple went on to become the most valuable company of all time. Of course, it did quite a few other things right as well!
On the other hand, history is littered with failed executives and companies that took risks too early and failed. Thus, the real challenge is constantly considering the options and choosing the right time where the risk-reward ratios look favorable. It’s not easy.
So my maxim is as follows:
A leader’s job is to constantly assess the risk-reward ratio of when the organization should pay the temporary performance penalty for jumping to an improved process, product, or service.
Share this Post